Half the Area of a Triangle

BJ Kim

Exploration

Given any triangle, we can bisect the area of triangle by using median.

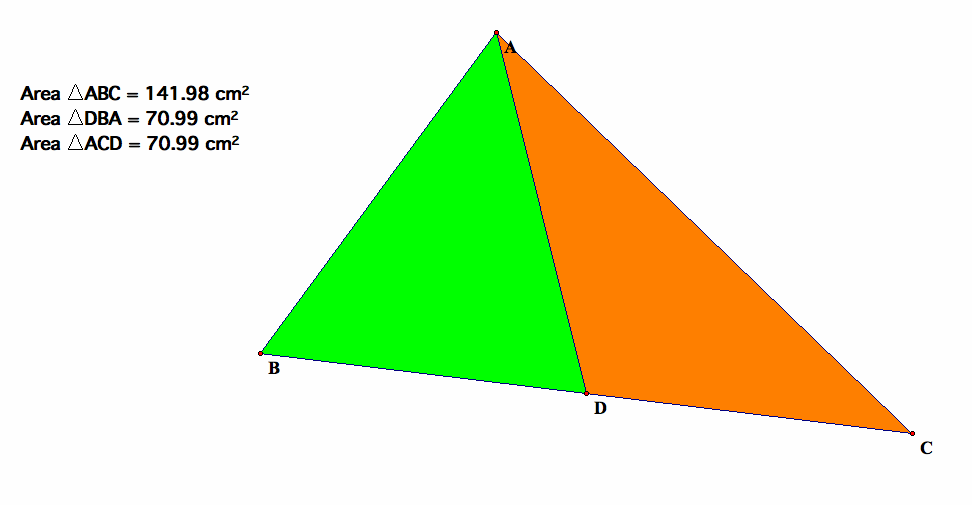
anytri

Let's start a problem 1.

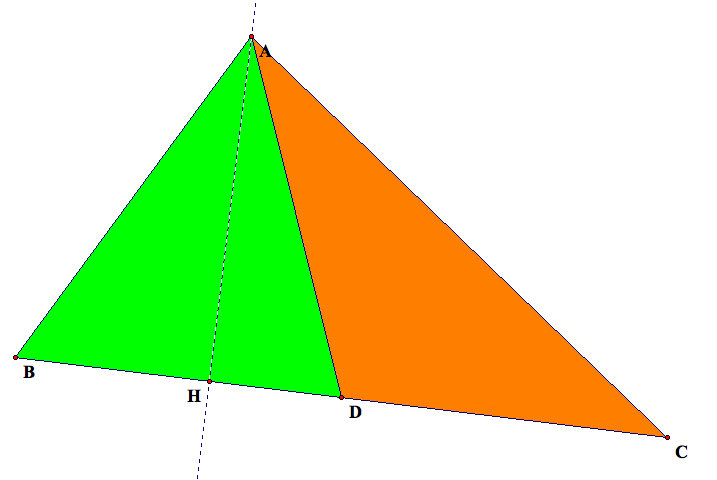
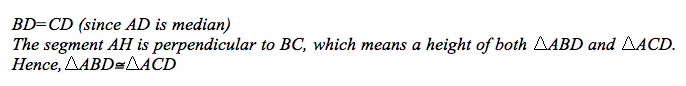
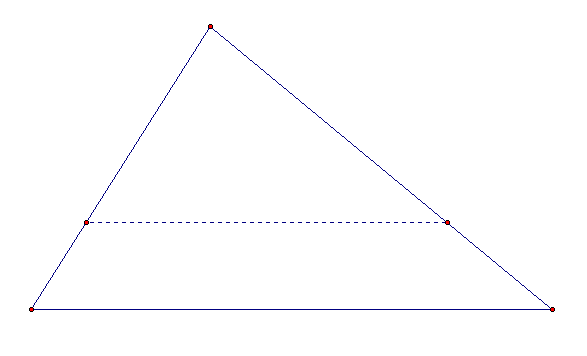
For any triangle, construct a segment parallel to a base of the triangle that devides the triangle into two equal areas.

instance

Question : If two similar figures have a ratio K of their areas, what is the ratio of the corresponding sides?

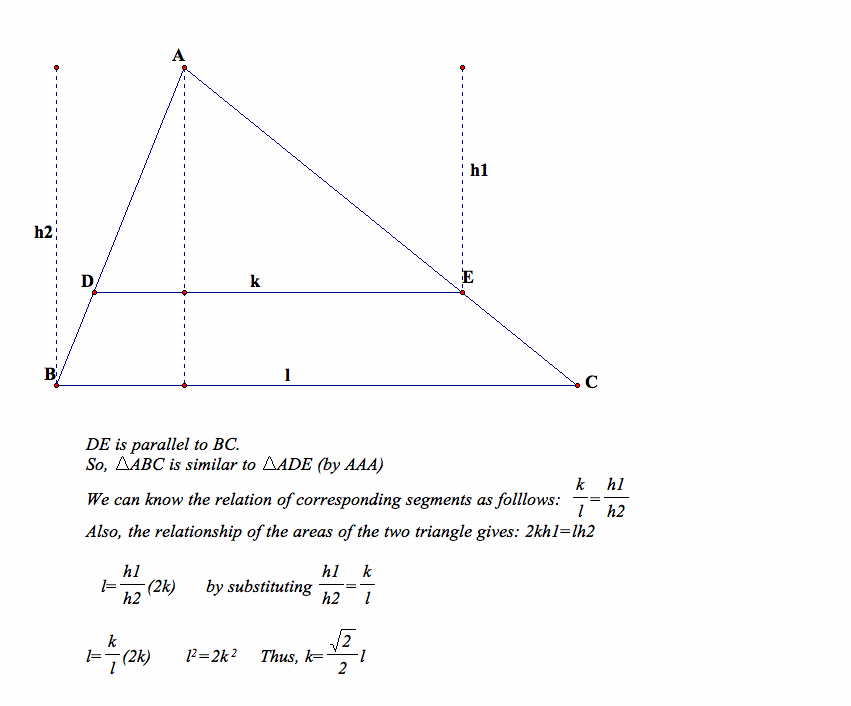
relation

Therefore, for the area of triangle ADE to be equal to half of the area of triangle ABC, the scale factor of k to l has to be 1 to the square root of 2.

In addition, if two similar figures have a ratio K of their areas, the ratio of the corresponding sides would be a square root of K.

Now, I would like to construct a segment parallel to a base of large triangle that devides the triangle into two equal areas.

By using DE:BC =1:square root of 2 (by above result), I can know the ratio of AD to AB is 1 to square root of 2 because of two similar triangles which have a ratio 2 of their areas. I want to make a 45-45-90 triangle with leg length the same as AD and the length of the hypotenuse will be the same as AB since the ratio of the legs to the hypotenuse of a 45-45-90 triangle is 1 to the square root of 2.

cons

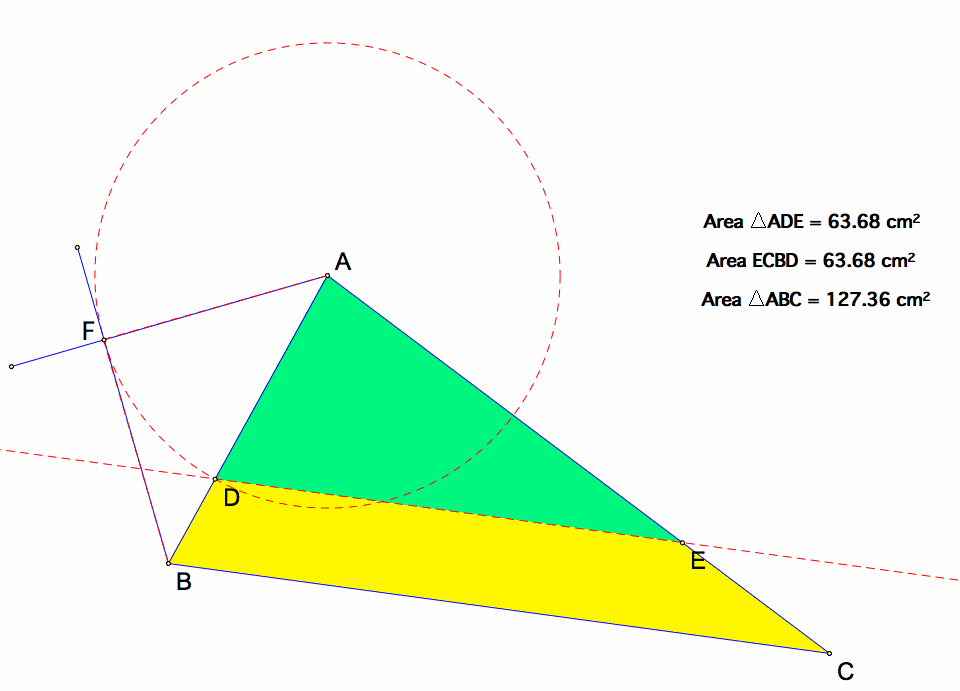
At first, rotate a segment AB, with center B, by 45 degees and rotate a segment AB, with center A, by -45 degrees. Their intersection would be a point F.

The triangle ABF is 45-45-90 triangle whose hypotenuse is AB. Make a circle with center A and radius AF. The intersection between the circle and AB would be a point D. Construct a parallel line to BC through D. Finally, we can see the segment DE.

Problem 2

Part A

If the parallel segment that divides the triangle into two equal areas is drawn for each base, a smaller triangle is formed. What is the ratio of the area of the small triangle to the original?

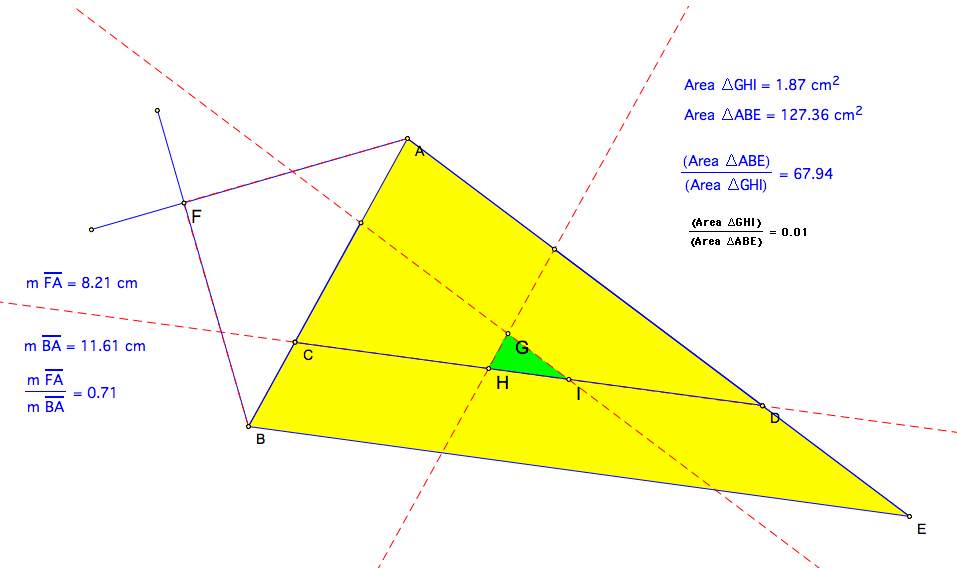
By investigations in GSP, I have found that the ratio between the green triangle and the yellow triangle is approximately 0.01.

Part B.

What is the ratio of the area of the green triangle to the area of the original triangle in the figure below? Here again the segments parallel to the bases divide the original triangles into two equal areas.

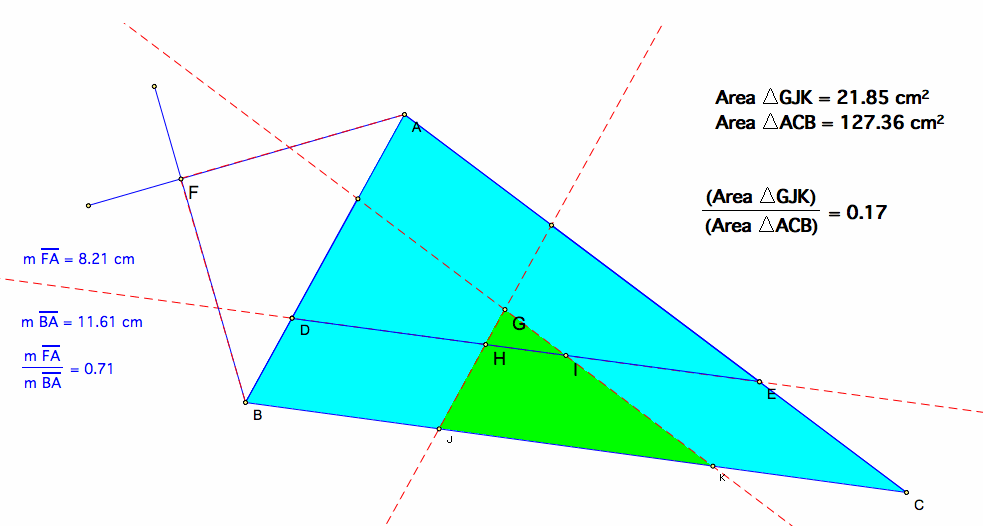
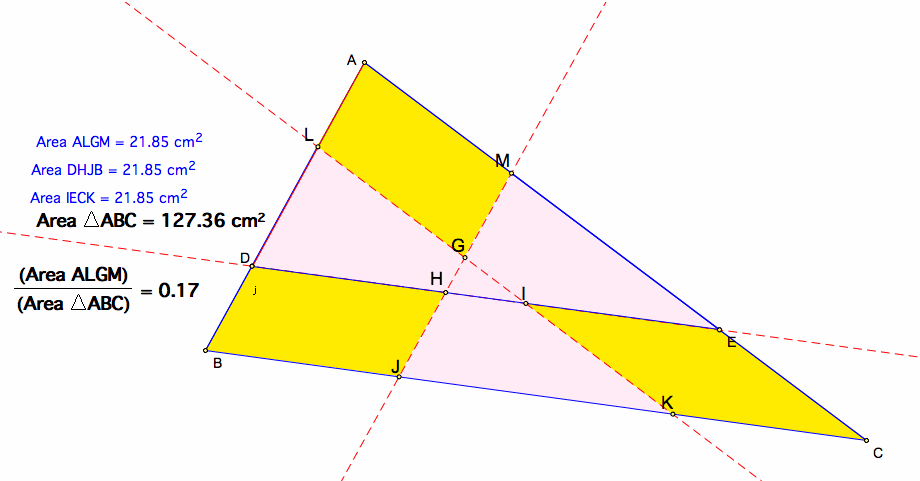
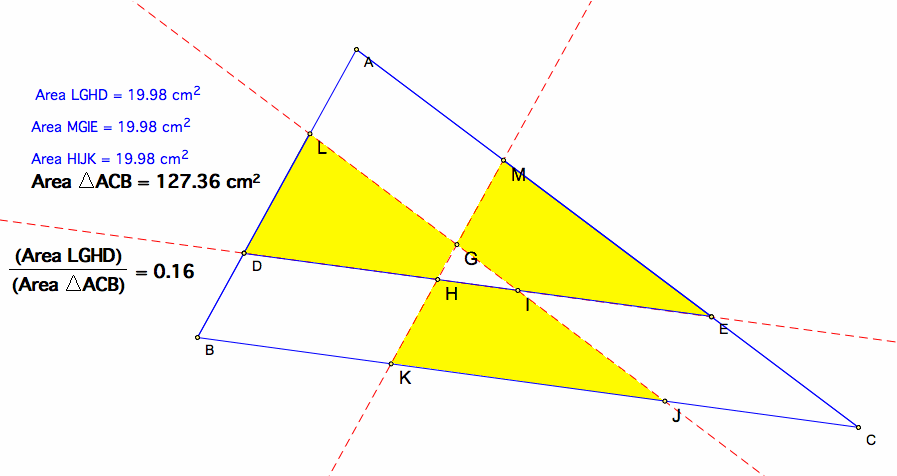
By investigations in GSP, I have found that the ratio between the green triangle and the large triangle is approximately 0.17.

Part C

Prove that the measures of the three shaded areas in each of the figures below are the same. In each figure what is the ratio of the area of one of the regions to the area of the original triangle?

Proof

Each shaded area is equal.(A=E=G and B=D=F)

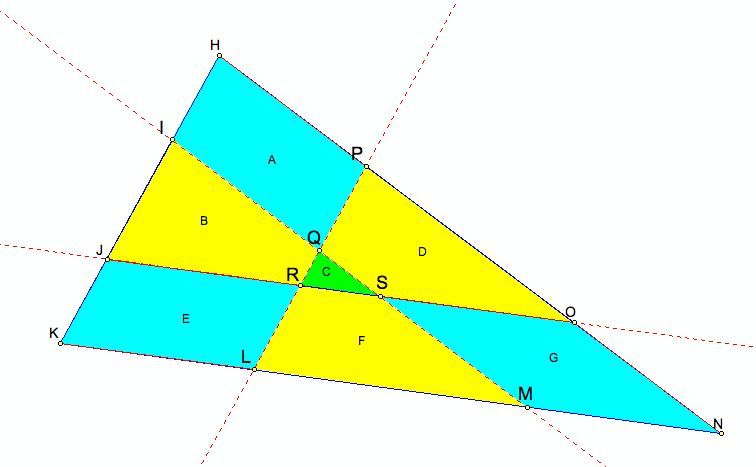
prove

Label each area such that A,B,C,D,E,F,G like above figure.

According to Half the area of the triangle, we can know that:

A+B+C+D=E+F+G
C+D+F+G=A+B+E
B+C+E+F=A+D+G

By regrouping,
A+B+C+D=A+B+E ==> E=C+D
C+D+F+G=A+D+G ==> A=C+F
B+C+E+F=E+F+G ==> G=C+B

To prove A=E=G,
First of all, we know A, E, and G are parallelogram since corresponding sides are parallel.
If the length of HO is t, then HN would be sqrt(2)t. Also, we can know when HN is sqrt(2)t ,PN would be t.
Hence, HO=NP. However, PO is common.
Therefore, HP=NO.
Since NH//MI, the height of two parallelogram(A and G) is the same. It means the area of parallelogram is equal,that is, A=G.Similarly,
If the length of LN is w, then KN would be sqrt(2)w. In addition, we can know when KN is sqrt(2)w ,KM would be w.
Hence, KM=LN. However, LM is common.
Therefore, KL=MN.
Since JO//KN, the height of two parallelogram(E and G) is the same. It means the area of parallelogram is equal,that is, E=G.Therefore, A=E=GThis implies B=D=F as well because our previous equations are E=C+D, A=C+F, G=C+B and C is common area.
Therefore, we have proven the three shaded areas are equal.
In other words, A=E=G (blue shaded), B=D=F (yellow shaded)

Part D.

Look at the various ratios you have found in parts A,B, and C. Are there any other relationships among areas or combinations of areas.

The ratio of a single trapezoid region, like B(.16), is the ratio of the parallelogram region(.17) in Part C minus the small triangle(.01) in Part A.

Thus, the ratio of the parallelogram regions (A, E, G) over the entire triangle is .17x3=.51.

The ratio of all trapezoid areas (B, D, F) over the entire triangle is .16x3=.48

The ratio of the smallest triangle(C) over the entire triangle would be 1-.51-.48=.01